Comment effectuer une analyse préliminaire des données ? (Statistiques & probabilités)

Il n’existe pas de réponse unique à cette question, car la meilleure façon de mener une analyse préliminaire des données varie en fonction du type et de la quantité de données disponibles, ainsi que des buts et objectifs spécifiques de l’analyse.
Toutefois, pour mener une analyse préliminaire des données efficace, nous verrons comment utiliser les concepts statistiques suivants :
- Statistiques descriptives
- Distributions de probabilités
- Intervalles de confiance
Introduction à l’analyse des données
Qu’est-ce qu’un ensemble de données ?
Un ensemble de données est une collection de données. Les données sont un ensemble de valeurs de sujets par rapport à des variables qualitatives ou quantitatives. Dans un ensemble de données, chaque valeur est un cas.
Qu’est-ce qu’un cas ?
Un cas est une unité unique d’une observation. Cela peut être une personne, une chose, un événement ou toute autre chose sur laquelle des informations sont collectées.
Dans la recherche, un cas est souvent une personne individuelle, mais il peut aussi s’agir d’une organisation, d’un groupe de personnes ou même d’un pays.
Qu’est-ce qu’une variable ?
Une variable est une mesure d’un sujet qui peut prendre différentes valeurs. Par exemple, l’âge est une variable qui peut prendre différentes valeurs telles que 20, 21, 22, etc.
Qu’est-ce qu’une variable qualitative ?
Une variable qualitative est une variable qui n’est pas numérique. Les variables qualitatives peuvent être observées et enregistrées mais pas mesurées, et elles existent sur une échelle qui est soit ordinale, soit par intervalle, soit par rapport.
Exemples de variables qualitatives
Voici quelques exemples de variables qualitatives :
- le sexe
- la race
- couleur
- le pays
- région
Qu’est-ce qu’une variable quantitative ?
Une variable quantitative est une variable qui est numérique. C’est une variable qui peut être comptée. La taille, le poids et l’âge sont des exemples de variables quantitatives.
Exemples de variables quantitatives
Quelques exemples de variables quantitatives sont :
- l’âge
- le poids
- la taille
- distance
- le temps
- vitesse
Qu’est-ce que l’analyse des données ?
L’analyse des données est le processus d’inspection, de nettoyage, de transformation et de modélisation des données dans le but de découvrir des informations utiles, de suggérer des conclusions et de soutenir la prise de décision.
L’analyse des données a de multiples facettes et approches, englobant diverses techniques sous une variété de noms, dans différents domaines comme celui des affaires, des sciences et des sciences sociales.
Statistiques descriptives
Les statistiques descriptives sont des méthodes statistiques utilisées pour résumer et décrire les données.
Les statistiques descriptives sont utilisées pour décrire les caractéristiques de base des données d’une étude. Elles fournissent des résumés sur l’échantillon et les mesures. Avec une analyse graphique simple, elles constituent la base de pratiquement toute analyse quantitative des données.
Les statistiques descriptives se distinguent des statistiques inférentielles, en ce sens que les statistiques descriptives visent à résumer les données, tandis que les statistiques inférentielles visent à caractériser la population dont proviennent les données.
Il existe trois principaux types de statistiques descriptives :
- Mesures de la tendance centrale
- Mesures de dispersion
- Mesures de la forme
Mesures de la tendance centrale
Les mesures de tendance centrale sont utilisées pour décrire le centre d’une distribution. Les mesures de tendance centrale sont utilisées pour décrire le centre d’une distribution. Cela peut se faire à l’aide d’une statistique simple, comme la moyenne, la médiane ou le mode, ou d’une statistique plus complexe, comme la moyenne ajustée ou la moyenne pondérée.
Les mesures de tendance centrale les plus courantes sont :
- la moyenne
- la médiane
- le mode
- la moyenne ajustée
La moyenne est la moyenne arithmétique d’un ensemble de valeurs, et est calculée en additionnant toutes les valeurs et en divisant par le nombre de valeurs.
La médiane est la valeur moyenne d’un ensemble de valeurs. Elle est calculée en classant toutes les valeurs de la plus petite à la plus grande, puis en choisissant la valeur qui se trouve au milieu. S’il y a un nombre pair de valeurs, la médiane est la moyenne des deux valeurs centrales.
Le mode est la valeur qui apparaît le plus souvent dans un ensemble de valeurs.
La moyenne ajustée est la moyenne de l’ensemble des données après qu’un certain pourcentage des données ait été supprimé. La moyenne pondérée est la moyenne de l’ensemble des données après que chaque valeur a été pondérée en fonction d’un certain critère.
Mesures de dispersion
Les mesures de dispersion sont utilisées pour décrire la dispersion d’une distribution. Les mesures de dispersion les plus courantes sont :
- l’étendue
- L’écart interquartile
- Écart-type
L’étendue est la différence entre les valeurs les plus grandes et les plus petites.
L’écart interquartile est la différence entre le premier et le troisième quartile.
L’écart-type est une mesure de la variabilité d’une distribution. On le calcule en prenant la racine carrée de la variance. La variance est la moyenne des écarts au carré par rapport à la moyenne.
Mesures de la forme
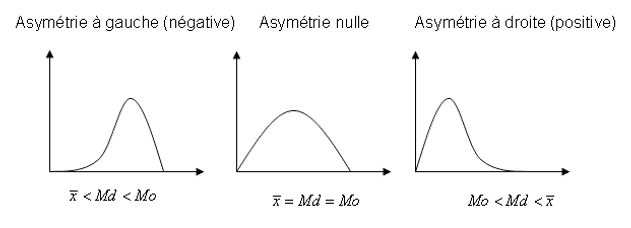
Les mesures de la forme sont utilisées pour décrire la forme générale d’une distribution. La mesure de la forme la plus courante est l’asymétrie.
L’asymétrie est une mesure de l’asymétrie d’une distribution. Une distribution est symétrique si elle est symétrique par rapport à son centre. Une distribution est asymétrique si elle n’est pas symétrique. (Porte ouverte enfoncée !)
Une distribution est positivement asymétrique si elle a une longue queue vers la droite. Une distribution est négativement asymétrique si elle a une longue queue vers la gauche.
Distributions de probabilités
Une distribution de probabilité est une fonction mathématique qui décrit la probabilité qu’une variable aléatoire prenne une valeur donnée. Dit autrement, une distribution de probabilité est une fonction qui attribue une probabilité à chaque valeur que peut prendre la variable aléatoire.
Une variable aléatoire est une variable dont la valeur n’est pas connue à l’avance, mais qui peut prendre n’importe quelle valeur parmi un ensemble de valeurs.
Il existe de nombreux types de distributions de probabilité, chacune ayant ses propres propriétés. Les types les plus courants de distributions de probabilité sont :
- les distributions discrètes
- Les distributions continues
Les distributions discrètes sont utilisées pour modéliser des variables qui ne peuvent prendre qu’un ensemble fini de valeurs. Les distributions continues sont utilisées pour modéliser des variables qui peuvent prendre n’importe quelle valeur dans un intervalle.
Distributions discrètes
Les distributions discrètes sont utilisées pour modéliser des variables qui ne peuvent prendre qu’un ensemble fini de valeurs. Les types les plus courants de distributions discrètes sont :
- la distribution de Bernoulli
- Distribution binomiale
- Distribution de Poisson
La distribution de Bernoulli est utilisée pour modéliser un résultat binaire, où le résultat ne peut prendre que l’une des deux valeurs.
La distribution binomiale est utilisée pour modéliser le nombre de réussites dans un nombre fixe d’essais, où le résultat de chaque essai est soit un succès, soit un échec.
La distribution de Poisson est utilisée pour modéliser le nombre d’événements au cours d’une période donnée, où l’événement peut se produire plusieurs fois au cours de la période.
Distributions continues
Les distributions continues sont utilisées pour modéliser des variables qui peuvent prendre n’importe quelle valeur dans un intervalle. Les types les plus courants de distributions continues sont :
- Distribution uniforme
- Distribution normale
- Distribution exponentielle
La distribution uniforme est utilisée pour modéliser les données qui sont uniformément réparties sur une plage.
La distribution normale est utilisée pour modéliser des données qui sont distribuées symétriquement autour d’une moyenne.
La distribution exponentielle est utilisée pour modéliser des données qui sont distribuées de manière asymétrique, avec une longue queue vers la droite.
Intervalles de confiance
Un intervalle de confiance est une plage de valeurs qui est susceptible de contenir la vraie valeur d’un paramètre de population.
Les intervalles de confiance sont utilisés pour estimer des paramètres de population à partir de données d’échantillon. Ils sont calculés à partir d’une estimation ponctuelle du paramètre de population et d’une mesure de la variabilité de l’estimation.
L’estimation ponctuelle est l’estimation du paramètre de population qui est calculée à partir des données de l’échantillon.
La mesure de la variabilité est utilisée pour quantifier l’incertitude de l’estimation ponctuelle. Les mesures les plus courantes de la variabilité sont l’erreur standard et la marge d’erreur :
- L’erreur standard est l’écart type de l’estimation ponctuelle.
- La marge d’erreur est la distance entre l’estimation ponctuelle et les limites supérieure et inférieure de l’intervalle de confiance.
Les intervalles de confiance sont généralement exprimés en pourcentage, comme l’intervalle de confiance de 95 %. On appelle cela le niveau de confiance.
Le niveau de confiance est la probabilité que l’intervalle de confiance contienne la vraie valeur du paramètre de la population.
Conclusion
Dans cette article, nous avons appris les bases de l’analyse des données. Nous avons découvert les différents types de données, les différents types de variables et les différents types de distributions. Nous avons également découvert les différents types de statistiques descriptives et la manière de les calculer. Enfin, nous avons appris à connaître les intervalles de confiance et à les calculer.
